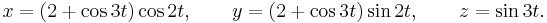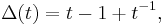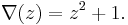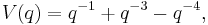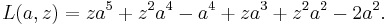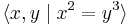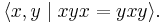Trefoil knot

In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory, which has diverse applications in topology, geometry, physics, and chemistry.

The trefoil knot is named after the three-leaf clover (or trefoil) plant.

1 Descriptions
2 Symmetry
3 Nontriviality
4 Classification
5 Invariants
6 Trefoils in religion and culture
7 See also
8 References
9 External links

Descriptions

The trefoil can be defined as the curve obtained from the following parametric equations:

$x = (2%2B\cos 3t)\cos 2t, \qquad y=(2%2B\cos 3t )\sin 2t, \qquad z=\sin 3t.$

This curve lies entirely on the torus 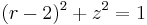$(r-2)^2%2Bz^2 = 1$ , making the trefoil the simplest example of a torus knot. (Specifically, the trefoil is the (2,3)-torus knot, since the curve winds around the torus three times in one direction and twice in the other direction.)

Any continuous deformation of the curve above is also considered a trefoil knot. Specifically, any curve isotopic to a trefoil knot is also considered to be a trefoil. In addition, the mirror image of a trefoil knot is also considered to be a trefoil. In topology and knot theory, the trefoil is usually defined using a knot diagram instead of an explicit parametric equation.

In algebraic geometry, the trefoil can also be obtained as the intersection in C² of the unit 3-sphere S³ with the complex plane curve of zeroes of the complex polynomial z² + w³ (a cuspidal cubic).

A left-handed trefoil and a right-handed trefoil.

Symmetry

The trefoil knot is chiral, in the sense that a trefoil knot can be distinguished from its own mirror image. The two resulting variants are known as the left-handed trefoil and the right-handed trefoil. It is not possible to deform a left-handed trefoil continuously into a right-handed trefoil, or vice-versa. (That is, the two trefoils are not isotopic.)

Though the trefoil knot is chiral, it is also invertible, meaning that there is no distinction between a counterclockwise-oriented trefoil and a clockwise-oriented trefoil. That is, the chirality of a trefoil depends only on the over and under crossings, not the orientation of the curve.

Nontriviality

The trefoil knot is nontrivial, meaning that it is not possible to “untie” a trefoil knot in three dimensions without cutting it. From a mathematical point of view, this means that a trefoil knot is not isotopic to the unknot. In particular, there is no sequence of Reidemeister moves that will untie a trefoil.

Proving this requires the construction of a knot invariant that distinguishes the trefoil from the unknot. The simplest such invariant is tricolorability: the trefoil is tricolorable, but the unknot is not. In addition, virtually every major knot polynomial distinguishes the trefoil from an unknot, as do most other strong knot invariants.

Classification

In knot theory, the trefoil is the first nontrivial knot, and is the only knot with crossing number three. It is a prime knot, and is listed as 3₁ in the Alexander-Briggs notation. The Dowker notation for the trefoil is 4 6 2, and the Conway notation for the trefoil is [3].

The trefoil can be described as the (2,3)-torus knot. It is also the knot obtained by closing the braid σ₁³.

The trefoil is an alternating knot. However, it is not a slice knot, meaning that it does not bound a smooth 2-dimensional disk in the 4-dimensional ball; one way to prove this is to note that its signature is not zero. Another proof is that its Alexander polynomial does not satisfy the Fox-Milnor condition.

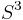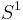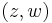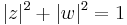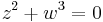The trefoil is a fibered knot, meaning that its complement in $S^3$ is a fiber bundle over the circle $S^1$ . In the model of the trefoil as the set of pairs $(z,w)$ of complex numbers such that $|z|^2%2B|w|^2=1$ and $z^2%2Bw^3=0$ , this fiber bundle has the Milnor map 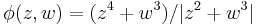$\phi(z,w)=( z^4%2Bw^3)/|z^2%2Bw^3|$ as its fibration, and a once-punctured torus as its fiber surface. Since the knot complement is Seifert fibred with boundary, it has a horizontal incompressible surface -- this is also the fiber of the Milnor map.

Invariants

The Alexander polynomial of the trefoil knot is

$\Delta(t) = t - 1 %2B t^{-1}, \,$

and the Conway polynomial is

$\nabla(z) = z^2 %2B 1.$ ^[1]

The Jones polynomial is

$V(q) = q^{-1} %2B q^{-3} - q^{-4}, \,$

and the Kauffman polynomial of the trefoil is

$L(a,z) = za^5 %2B z^2a^4 - a^4 %2B za^3 %2B z^2a^2-2a^2. \,$

The knot group of the trefoil is given by the presentation

$\langle x,y \mid x^2=y^3 \rangle \,$

or equivalently

$\langle x,y \mid xyx=yxy \rangle. \,$ ^[2]

This group is isomorphic to the braid group with three strands.

Trefoils in religion and culture

As the simplest nontrivial knot, the trefoil is a common motif in iconography and the visual arts. For example, the common form of the triquetra symbol is a trefoil, as are some versions of the Germanic Valknut.

Trefoil knots

A simple triquetra symbol

A tightly-knotted triquetra

The Germanic Valknut

A metallic Valknut in the shape of a trefoil

In modern art, the woodcut “Knots” by M. C. Escher depicts three trefoil knots whose solid forms are twisted in different ways.^[3]

References

^ 3 1 - Knot Atlas
^ Weisstein, Eric W. "Trefoil Knot." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/TrefoilKnot.html
^ The Official M.C. Escher Website — Gallery — “Knots”

External links

Wolframalpha: (2,3)-torus knot